Narrow DES
I came up with this slender DES variant that is made for a 48 bit architecture.
Hint: the flag is the key in hex, wrapped in ENO{...}
new hint: We could have done a thousand rounds and the attack would not get more difficult.
The running time of a solution script is rather measured in minutes, instead of seconds.
nc 52.59.124.14 5031 This is my first time to get First Blood and the only solve.

Attachment contains the following code:
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <string.h>
#define LB32_MASK 0x00000000ffffffff
#define LB24_MASK 0x0000000000ffffff
#define ROUNDS 32
/* Post S-Box permutation */
static char P[] = {
8, 18, 3, 2, 15, 24, 10, 14, 20, 7, 5, 13, 1, 6, 21, 9, 4, 11, 23, 22, 12, 19, 16, 17
};
/* The S-Box tables */
static char S[8][16] = {{
5, 3, 0, 2, 7, 1, 4, 6,
1, 6, 4, 7, 5, 0, 3, 2,
}, {
4, 1, 0, 5, 3, 7, 6, 2,
1, 4, 0, 5, 2, 6, 3, 7,
}, {
3, 4, 2, 0, 7, 6, 1, 5,
3, 7, 6, 0, 4, 2, 1, 5,
}, {
5, 6, 4, 2, 7, 0, 3, 1,
6, 5, 7, 2, 1, 3, 4, 0,
}, {
5, 6, 7, 3, 1, 0, 4, 2,
3, 6, 2, 1, 7, 4, 0, 5,
}, {
0, 3, 1, 4, 6, 5, 2, 7,
0, 3, 5, 4, 7, 6, 1, 2,
}, {
6, 0, 4, 2, 3, 5, 1, 7,
0, 6, 7, 3, 2, 1, 4, 5,
}, {
0, 5, 6, 2, 3, 7, 4, 1,
2, 4, 0, 7, 3, 1, 5, 6,
}};
uint64_t des(uint64_t msg, uint64_t key, char mode) {
int i, j;
uint32_t L = 0;
uint32_t R = 0;
uint32_t expanded = 0;
uint32_t s_output = 0;
uint32_t p_output = 0;
uint32_t temp = 0;
uint32_t sub_key[2] = {0};
L = (uint32_t)((msg >> 24) & LB24_MASK);
R = (uint32_t)(msg & LB24_MASK);
/* Calculation of the 16 keys */
sub_key[0] = (uint32_t)(key >> 32);
sub_key[1] = (uint32_t)(key & LB32_MASK);
for (i = 0; i < ROUNDS; i++) {
expanded = 0;
for (j = 0; j < 7; j++) {
expanded |= ((R >> (20 - 3*j)) & 0xf) << (28 - 4*j);
}
expanded |= (R & 7) << 1 | (R >> 23);
if (mode == 'd') {
expanded = expanded ^ sub_key[(i+1) % 2];
} else {
expanded = expanded ^ sub_key[i % 2];
}
s_output = 0;
for (j = 0; j < 8; j++) {
temp = (expanded >> (4*j)) & 0xf;
s_output <<= 3;
s_output |= (uint32_t) (S[j][temp]);
}
p_output = 0;
for (j = 0; j < 24; j++) {
p_output <<= 1;
p_output |= (s_output >> (24 - P[j])) & 1;
}
temp = R;
R = L ^ p_output;
L = temp;
}
return ((uint64_t) L) << 24 | R;
}
int main(int argc, const char * argv[]) {
char inputStr[769];
uint64_t key = 0x00000000;
printf("Give your message in hexadecimal.\n");
fflush(stdout);
uint64_t input, result;
char msg[13];
msg[12] = 0;
while(1) {
scanf("%768s" , inputStr);
for(int i = 0; i < 64; i++) {
memcpy(msg, inputStr + 12*i, 12);
input = (uint64_t)strtoull(msg, NULL, 16);
result = des(input, key, 'e');
printf("%012lx", result);
}
printf("\n");
fflush(stdout);
}
exit(0);
}The code implements a custom DES implementaion that:
- Uses a 64-bit key, where the lower/higher 32 bits are used for the subkeys in turn
- Encrypts/decrypts user-provided 48-bit data for 32 rounds
It is prone to Slide Attack Section 4 Modified DES Example: 2K-DES, due to the way how subkeys are used:
- If we refer to the lower 32 bits of the 64-bit key as
key1, the higher 32 bits askey0, then the custom DES implementation is essentially doing the Feistel computation for 32 rounds withkey0, key1, key0, key1, ..., key0, key1 - Choose a input (anything is okay), and send it to the server, so we know the result after 32 roudns of Feistel computation with
key0, key1, key0, key1, ..., key0, key1 - By enumerating 32-bit
key1, we can go one step back, to compute the Feistel computation for 31 rounds without the last key1:key0, key1, key0, key1, ..., key0 - Then, we send the value to the server to ask it to encrypt the value. The server encrypts it by running 32 rounds of Feistel computation with
key0, key1, key0, key1, ..., key0, key1. - Since the Feistel computation is reversible/cancelable (due to its XOR nature), the keys cancel out:
key0, key1, key0, key1, ..., key0, key0, key1, key0, key1, ..., key0, key1becomeskey1, so the result is only one step from the original input - We can verify that, if the result is actually one step from the original input given
key1(also utilize the fact thatRbecomes nextLin the Feistel computation to speed up), we know a possiblekey1. Then, we can bruteforce 32-bitkey2.
The process is shown in the following figure, taken from Slide Attack Figure 2:
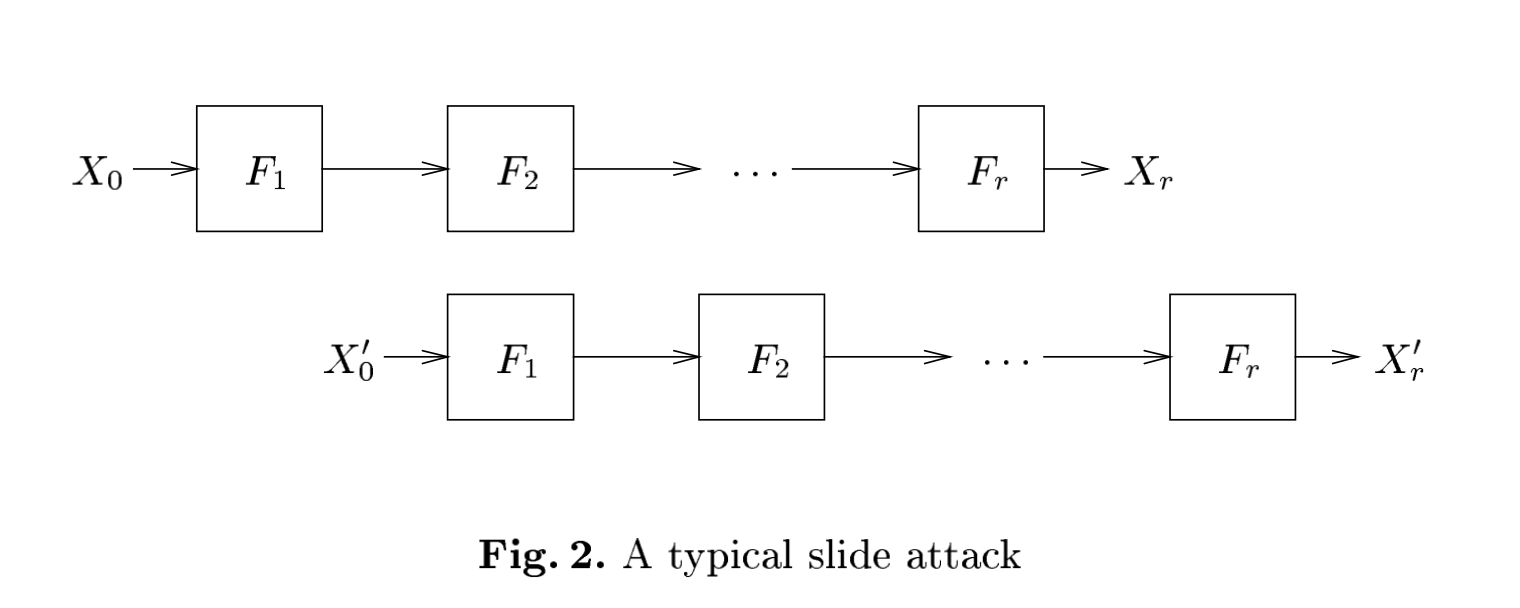
We are going forward 32 steps, back for one step, back for 32 steps and verify that going one step forward gives us the correct answer.
Let's make a proof of concept locally, by using a small key (0x00004321 || 0x00005678) and attack locally:
#include <assert.h>
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#define LB32_MASK 0x00000000ffffffff
#define LB24_MASK 0x0000000000ffffff
#define ROUNDS 32
/* Post S-Box permutation */
static char P[] = {8, 18, 3, 2, 15, 24, 10, 14, 20, 7, 5, 13,
1, 6, 21, 9, 4, 11, 23, 22, 12, 19, 16, 17};
/* The S-Box tables */
static char S[8][16] = {{
5, 3, 0, 2, 7, 1, 4, 6,
1, 6, 4, 7, 5, 0, 3, 2,
}, {
4, 1, 0, 5, 3, 7, 6, 2,
1, 4, 0, 5, 2, 6, 3, 7,
}, {
3, 4, 2, 0, 7, 6, 1, 5,
3, 7, 6, 0, 4, 2, 1, 5,
}, {
5, 6, 4, 2, 7, 0, 3, 1,
6, 5, 7, 2, 1, 3, 4, 0,
}, {
5, 6, 7, 3, 1, 0, 4, 2,
3, 6, 2, 1, 7, 4, 0, 5,
}, {
0, 3, 1, 4, 6, 5, 2, 7,
0, 3, 5, 4, 7, 6, 1, 2,
}, {
6, 0, 4, 2, 3, 5, 1, 7,
0, 6, 7, 3, 2, 1, 4, 5,
}, {
0, 5, 6, 2, 3, 7, 4, 1,
2, 4, 0, 7, 3, 1, 5, 6,
}};
uint64_t des(uint64_t msg, uint64_t key, char mode, int rounds) {
int i, j;
uint32_t L = 0;
uint32_t R = 0;
uint32_t expanded = 0;
uint32_t s_output = 0;
uint32_t p_output = 0;
uint32_t temp = 0;
uint32_t sub_key[2] = {0};
L = (uint32_t)((msg >> 24) & LB24_MASK);
R = (uint32_t)(msg & LB24_MASK);
/* Calculation of the 16 keys */
sub_key[0] = (uint32_t)(key >> 32);
sub_key[1] = (uint32_t)(key & LB32_MASK);
for (i = 0; i < rounds; i++) {
expanded = 0;
for (j = 0; j < 7; j++) {
expanded |= ((R >> (20 - 3 * j)) & 0xf) << (28 - 4 * j);
}
expanded |= (R & 7) << 1 | (R >> 23);
if (mode == 'd') {
expanded = expanded ^ sub_key[(i + 1) % 2];
// printf("%c %d in L:%lx R:%lx exp:%lx key:%lx\n", mode, i, L, R,
// expanded, sub_key[(i + 1) % 2]);
} else {
expanded = expanded ^ sub_key[i % 2];
// printf("%c %d in L:%lx R:%lx exp:%lx key:%lx\n", mode, i, L, R,
// expanded,
// sub_key[i % 2]);
}
s_output = 0;
for (j = 0; j < 8; j++) {
temp = (expanded >> (4 * j)) & 0xf;
s_output <<= 3;
s_output |= (uint32_t)(S[j][temp]);
}
p_output = 0;
for (j = 0; j < 24; j++) {
p_output <<= 1;
p_output |= (s_output >> (24 - P[j])) & 1;
}
temp = R;
R = L ^ p_output;
L = temp;
// printf("%c %d out L:%lx R:%lx\n", mode, i, L, R);
}
return ((uint64_t)L) << 24 | R;
}
int main(int argc, const char *argv[]) {
uint64_t key = 0x0000876500004321;
// result = enc(input, key)
uint64_t input = 0x0000cba987654321; // arbitrary 48-bit input
uint64_t result = des(input, key, 'e', ROUNDS);
for (uint64_t key1 = 0x0; key1 <= (1L << 32); key1++) {
// guess low 24 bit of key
// go back one
uint64_t result_rev = (result >> 24) | ((result & LB24_MASK) << 24);
uint64_t temp = des(result_rev, key1, 'd', 1);
// encrypt temp
uint64_t enc_temp = des(temp, key, 'e', ROUNDS);
// it should have half equal to the input
if ((enc_temp >> 24) == (input >> 24)) {
fprintf(stderr, "possible key1 %lx\n", key1);
uint64_t enc_temp_rev = (enc_temp >> 24) | ((enc_temp & LB24_MASK) << 24);
// find first half
for (uint64_t key2 = 0x0; key2 <= (1L << 32); key2++) {
uint64_t guess_key = (key2 << 32) | key1;
uint64_t temp2 = des(enc_temp_rev, guess_key, 'd', 1);
if (temp2 == input && des(input, guess_key, 'e', ROUNDS) == result) {
fprintf(stderr, "found key %lx\n", guess_key);
return 0;
}
}
}
}
return 0;
}Output:
possible key1 4321
found key 876500004321It can correctly recover the key.
So the next step is to interact with the server. In the previous version, we need to send 2^32 messages to the server, which is slow, even though I create a VPS in AWS eu-central-1 region. Some optimizations must be applied:
- Batch sending: Prepare everything to send, and receive them in the VPS
- Reduce messages by find the
2^24possible intermediate values: instead of enumerating all2^32keys, actuall only2^24different messages can be sent to the server, since the other halfRof Feistel computation is fixed - Split the networking and computation part: Send
2^24messages, filter out possible ones on the VPS, then do the heavy lifting on a local server.
After sending 2^24 messages to the server, I found that only two possible values are found for the intermediate value:
possible low aa86d1
possible low ea4992Both of them might lead to multiple key1 possibilities, like:
possible low aa86d1
possible key1 5240fce5
possible key1 5240fce9
possible key1 524bfce5
possible key1 524bfce9This is not a large number, though. So I just bruteforced all these possiblities on a AMD EPYC server in parallel:
#include <assert.h>
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#define LB32_MASK 0x00000000ffffffff
#define LB24_MASK 0x0000000000ffffff
#define ROUNDS 32
/* Post S-Box permutation */
static char P[] = {8, 18, 3, 2, 15, 24, 10, 14, 20, 7, 5, 13,
1, 6, 21, 9, 4, 11, 23, 22, 12, 19, 16, 17};
/* The S-Box tables */
static char S[8][16] = {{
5, 3, 0, 2, 7, 1, 4, 6,
1, 6, 4, 7, 5, 0, 3, 2,
}, {
4, 1, 0, 5, 3, 7, 6, 2,
1, 4, 0, 5, 2, 6, 3, 7,
}, {
3, 4, 2, 0, 7, 6, 1, 5,
3, 7, 6, 0, 4, 2, 1, 5,
}, {
5, 6, 4, 2, 7, 0, 3, 1,
6, 5, 7, 2, 1, 3, 4, 0,
}, {
5, 6, 7, 3, 1, 0, 4, 2,
3, 6, 2, 1, 7, 4, 0, 5,
}, {
0, 3, 1, 4, 6, 5, 2, 7,
0, 3, 5, 4, 7, 6, 1, 2,
}, {
6, 0, 4, 2, 3, 5, 1, 7,
0, 6, 7, 3, 2, 1, 4, 5,
}, {
0, 5, 6, 2, 3, 7, 4, 1,
2, 4, 0, 7, 3, 1, 5, 6,
}};
uint64_t des(uint64_t msg, uint64_t key, char mode, int rounds) {
int i, j;
uint32_t L = 0;
uint32_t R = 0;
uint32_t expanded = 0;
uint32_t s_output = 0;
uint32_t p_output = 0;
uint32_t temp = 0;
uint32_t sub_key[2] = {0};
L = (uint32_t)((msg >> 24) & LB24_MASK);
R = (uint32_t)(msg & LB24_MASK);
/* Calculation of the 16 keys */
sub_key[0] = (uint32_t)(key >> 32);
sub_key[1] = (uint32_t)(key & LB32_MASK);
for (i = 0; i < rounds; i++) {
expanded = 0;
for (j = 0; j < 7; j++) {
expanded |= ((R >> (20 - 3 * j)) & 0xf) << (28 - 4 * j);
}
expanded |= (R & 7) << 1 | (R >> 23);
if (mode == 'd') {
expanded = expanded ^ sub_key[(i + 1) % 2];
// printf("%c %d in L:%lx R:%lx exp:%lx key:%lx\n", mode, i, L, R,
// expanded, sub_key[(i + 1) % 2]);
} else {
expanded = expanded ^ sub_key[i % 2];
// printf("%c %d in L:%lx R:%lx exp:%lx key:%lx\n", mode, i, L, R,
// expanded,
// sub_key[i % 2]);
}
s_output = 0;
for (j = 0; j < 8; j++) {
temp = (expanded >> (4 * j)) & 0xf;
s_output <<= 3;
s_output |= (uint32_t)(S[j][temp]);
}
p_output = 0;
for (j = 0; j < 24; j++) {
p_output <<= 1;
p_output |= (s_output >> (24 - P[j])) & 1;
}
temp = R;
R = L ^ p_output;
L = temp;
// printf("%c %d out L:%lx R:%lx\n", mode, i, L, R);
}
return ((uint64_t)L) << 24 | R;
}
uint64_t get_time_ns() {
struct timespec ts;
clock_gettime(CLOCK_MONOTONIC, &ts);
return (uint64_t)ts.tv_sec * 1000000000 + (uint64_t)ts.tv_nsec;
}
uint64_t get_des_from_remote(uint64_t input) {
printf("%12lx\n", input);
fflush(stdout);
uint64_t result = 0;
while (1) {
char buffer[1024];
fgets(buffer, sizeof(buffer), stdin);
if (strlen(buffer) == 768 + 1) {
buffer[12] = 0;
sscanf(buffer, "%lx", &result);
break;
}
}
return result;
}
void get_many_des_from_remote(uint64_t *input, uint64_t *result, int count) {
assert(count % 64 == 0);
for (int i = 0; i < count; i++) {
printf("%012lx", input[i]);
}
printf("\n");
fflush(stdout);
char msg[13];
msg[12] = 0;
int progress = 0;
while (progress < count) {
char buffer[1024];
fgets(buffer, sizeof(buffer), stdin);
if (strlen(buffer) == 768 + 1) {
for (int i = 0; i < 64; i++) {
memcpy(msg, buffer + 12 * i, 12);
result[i + progress] = (uint64_t)strtoull(msg, NULL, 16);
}
progress += 64;
}
}
}
int main(int argc, const char *argv[]) {
// result = enc(input, key)
uint64_t input = 0x0000cba987654321; // 48-bit input
// uint64_t result = des(input, key, 'e', ROUNDS);
uint64_t result = get_des_from_remote(input);
#define BLOCK_SIZE 64
// for (uint64_t block = 0xea4980; block <= (1L << 24); block += BLOCK_SIZE) {
for (uint64_t block = 0xaa8600; block <= (1L << 24); block += BLOCK_SIZE) {
if (block % 0x10000 == 0) {
fprintf(stderr, "Testing key 0x%lx\n", block);
}
uint64_t inputs[BLOCK_SIZE];
uint64_t results[BLOCK_SIZE];
for (int i = 0; i < BLOCK_SIZE; i++) {
uint64_t low = block + i;
// guess low 24 bit of key
// go back one
// uint64_t result_rev = (result >> 24) | ((result & LB24_MASK) << 24);
// uint64_t temp = des(result_rev, key1, 'd', 1);
inputs[i] = (((result >> 24) & LB24_MASK) << 24) | low;
}
get_many_des_from_remote(inputs, results, BLOCK_SIZE);
for (int i = 0; i < BLOCK_SIZE; i++) {
uint64_t low = block + i;
uint64_t enc_temp = results[i];
// it should have half equal to the input
if ((enc_temp >> 24) == (input >> 24)) {
uint64_t enc_temp_rev =
(enc_temp >> 24) | ((enc_temp & LB24_MASK) << 24);
fprintf(stderr, "possible low %lx\n", low);
uint64_t key1 = 0;
// for (key1 = 0x5240fce0; key1 <= (1L << 32); key1++) {
for (key1 = 0x524bfce9; key1 <= (1L << 32); key1++) {
uint64_t result_rev = (result >> 24) | ((result & LB24_MASK) << 24);
uint64_t temp = des(result_rev, key1, 'd', 1);
if (temp == inputs[i]) {
uint64_t guess_key = key1;
uint64_t temp2 = des(enc_temp_rev, guess_key, 'd', 1);
if (temp2 != input) {
// validation failed
continue;
}
fprintf(stderr, "possible key1 %lx\n", key1);
guess_key = key1;
temp2 = des(enc_temp_rev, guess_key, 'd', 1);
// find first half
#pragma omp parallel for
for (uint64_t key2 = 0x0; key2 <= (1L << 32); key2++) {
uint64_t guess_key = (key2 << 32) | key1;
if (temp2 == input &&
des(input, guess_key, 'e', ROUNDS) == result) {
fprintf(stderr, "guess key %lx\n", guess_key);
}
}
fprintf(stderr, "done\n");
}
}
fprintf(stderr, "done\n");
}
}
}
return 0;
}Get flag after ~1 minute if we know the correct intermediate value and key1:
$ gcc -fopenmp attack.c -o attack -O2 && socat SYSTEM:./attack TCP:52.59.124.14:5031
possible low aa86d1
possible key1 524bfce9
guess key b3f7a549524bfce9
doneThe whole time is longer: enumerate intermediate values first, then for each intermediate value, enumerate key1 and for each key1 enumerate key2. It's fortunate that each step only takes several minutes if you get it right in a proper machine.
So the flag is ENO{b3f7a549524bfce9}. In summary:
- The slide attack reduces the attack complexity from
2^64to2^32 - By enumerating
2^24possibleLvalues, we remove the bottleneck on networking - Finish the last bruteforce locally in parallel