计算机图形学

本文参考了如下网站：

齐次坐标

齐次坐标是在 3 维的坐标 \((x, y, z)\) 的基础上，添加一维，变成 \((x, y, z, w)\)，对应 3 维的 \((x/w, y/w, z/w)\)，这样做可以方便一些计算。

因此从 3 维坐标转换为齐次坐标的时候，添加一维 \(w = 1\)，变成 \((x, y, z, 1)\)。为了让 3 维的向量和点在齐次坐标下可以进行运算，可以向 3 维向量添加一维 \(w=0\)，此时 \(w=0\) 表示向量，\(w \ne 0\) 表示点。

坐标变换

OpenGL 中坐标变换经过了如下的步骤：

物体坐标，4D 齐次坐标
乘以 Model 和 View 矩阵，得到 4D 齐次坐标
乘以 Projection 矩阵，得到 4D 齐次坐标
把齐次坐标转换为对应的 3D 坐标，为 Normalized Device Coordinates
把 3D 坐标对应到屏幕上的 2D 坐标

参考：OpenGL Transformation

Normalized Device Coordinates

NDC（Normalized Device Coordinates）是经过一系列变换以后，得到的最终的 3D 坐标。

以 OpenGL 为例，NDC 就是一个在三个坐标轴上都在 \([-1, 1]\) 之间的立方体，只有在这个立方体中的物体才可能被显示出来。

NDC 的坐标范围在不同的图形 API 下可能不一样，例如 OpenGL 和 WebGL 是从 \((-1, -1, -1)\) 到 \((1, 1, 1)\)，而 DirectX-12、Metal、Vulkan 和 WebGPU 是从 \((-1, -1, 0)\) 到 \((1, 1, 1)\)，也就是 Z 轴上的范围只有 \([0, 1]\)。

最后显示在屏幕上的时候，显示区域的左下角就对应 \(x=-1, y=-1\)，右上角对应 \(x=1, y=1\)（也可能是左上角 \(x=-1, y=-1\)，右下角 \(x=1, y=1\)，不同的图形 API 规定不同）。\(z\) 轴对应深度，显示在前面的（\(z\) 较小的）会遮挡显示在后面的（\(z\) 较大的）。

因此 NDC 到屏幕坐标的对应关系是：

x 轴：-1 -> x, 1 -> x + w
y 轴：-1 -> y, 1 -> y + w
z 轴：-1 -> n, 1 -> f

其中 x, y, w 和 h 用 glViewport 函数设置，n 和 f 用 glDepthRange 设置。

正交投影

正交投影要做的是把一个长方体线性映射到 NDC 中，以 OpenGL 为例，也就是要映射到三个维度上都是 \([-1, 1]\) 之间的立方体。

这个长方体的边和坐标轴平行，因此可以用以下几个变量来定义长方体的坐标：

left, right, top, bottom：定义了长方体上平行于 X-Y 屏幕的面的位置，其中 left 和 right 就是 X 轴上的最小值和最大值，bottom 和 top 就是 Y 轴上的最小值和最大值
near，far：定义了长方体在 Z 轴上的区间，离原点最近的平面的 Z 值是 -near，最远的平面的 Z 值是 -far

下面用这些坐标的首字母来简称：\(l\) 代表 left，依此类推。

目标是把这个长方体映射到 \([-1, 1]\) 的立方体上。

首先考虑 X 轴：要线性地把 \(x=l\) 映射到 \(x=-1\)，把 \(x=r\) 映射到 \(x=1\)，可以得到 \(x' = \frac{2}{r-l}x-\frac{r+l}{r-l}\)。

同理，Y 坐标的计算公式是 \(y' = \frac{2}{t-b}y-\frac{t+b}{t-b}\)。

Z 轴上多了一个负号：线性地把 \(z=-n\) 映射到 \(z=-1\)，把 \(z=-f\) 映射到 \(z=1\)，得到 \(z' = \frac{-2}{f-n}z-\frac{f+n}{f-n}\)。

注：如果 NDC 的 Z 轴范围是 \([0, 1]\)，那么 Z 轴的计算公式就是 \(z' = \frac{-1}{f-n}z-\frac{n}{f-n}\)

总结一下就是：

\[\begin{align} x' = \frac{2}{r-l}x-\frac{r+l}{r-l} \\ y' = \frac{2}{t-b}y-\frac{t+b}{t-b} \\ z' = \frac{-2}{f-n}z-\frac{f+n}{f-n} \end{align}\]

考虑到实际采用的是齐次坐标系，\(w\) 不变，所以 \(w' = w\)。把上面的等式写成矩阵的形式，就是：

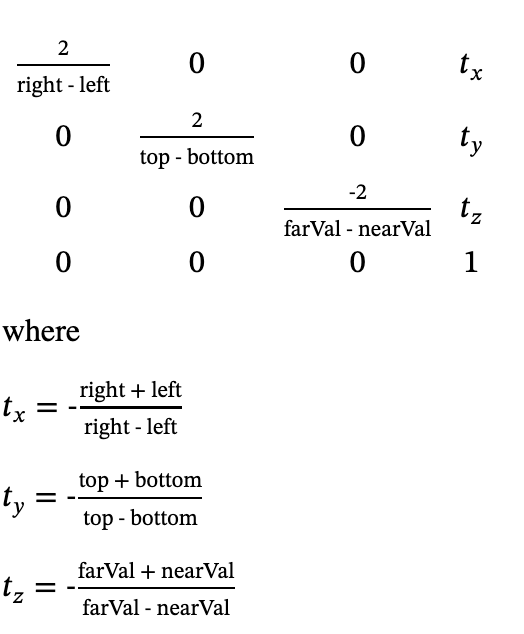
\[ \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{-2}{f-n} & -\frac{f+n}{f-n} \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

这正是 OpenGL 正交投影函数 glOrtho() 所计算的矩阵：

mesa 中的实现：

// Source: https://github.com/Mesa3D/mesa/blob/957009978ef6d7121fc0d710d03bc20097d4d46b/src/mesa/math/m_matrix.c#L813C1-L840
void
_math_float_ortho(float *m,
                  float left, float right,
                  float bottom, float top,
                  float nearval, float farval)
{
#define M(row,col)  m[col*4+row]
   M(0,0) = 2.0F / (right-left);
   M(0,1) = 0.0F;
   M(0,2) = 0.0F;
   M(0,3) = -(right+left) / (right-left);

   M(1,0) = 0.0F;
   M(1,1) = 2.0F / (top-bottom);
   M(1,2) = 0.0F;
   M(1,3) = -(top+bottom) / (top-bottom);

   M(2,0) = 0.0F;
   M(2,1) = 0.0F;
   M(2,2) = -2.0F / (farval-nearval);
   M(2,3) = -(farval+nearval) / (farval-nearval);

   M(3,0) = 0.0F;
   M(3,1) = 0.0F;
   M(3,2) = 0.0F;
   M(3,3) = 1.0F;
#undef M
}

透视投影

透视投影要做的是把一个四棱台（Square Frustum，四棱锥水平切开，底面和顶面是正方形，其余四个面都是梯形）映射到 NDC 上。其中四棱台的四条棱延长以后，交于原点。也就是说焦点就是坐标轴的原点。

相比正交投影，透视投影最大的不同在于它近大远小的特性，更加贴近实际：正交投影无论深度多少，看到的物体大小不变；而在透视投影中，从原点出发，到 near 平面上的一点连成射线，这条射线上的点都对应同一个屏幕上的点，因此远的物体在屏幕上看的小，近的物体在屏幕上看得大。

因此在实现透视投影的时候，就要利用这条从原点出发到 near 平面的一点的射线：由于这条射线上的点都对应屏幕上同一个点，因此在 NDC 中也对应同一个 \((x', y')\) 坐标。那么，在计算 \(x'\) 和 \(y'\) 的时候，先利用相似三角形关系，把点映射到 near 平面上（near 平面的 Z 坐标是 \(z=-n\)）：

\[\begin{align} \frac{x'}{x} = \frac{-n}{z} \\ \frac{y'}{y} = \frac{-n}{z} \end{align}\]

这样就得到了四棱台到长方体的映射，但是这里涉及到对 \(z\) 的除法运算，为了在矩阵中实现针对 \(z\) 的除法运算，需要利用齐次坐标自带的除法：\((x, y, z, w) \to (x/w, y/w, z/w)\)，也就是说，把 \(z\) 的值挪到 \(w\) 上，就相当于实现了除法。按照这个思路，可以得到下面的矩阵：

\[ \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & A & B \\ 0 & 0 & -1 & 0 \end{pmatrix} \]

其中 \(A\) 和 \(B\) 是未知数。验证一下上面的矩阵是否实现了除法：

首先是生成齐次坐标：

\[ (x, y, z) \to (x, y, z, 1) \]

矩阵变换以后：

\[\begin{align} x' &= nx \\ y' &= ny \\ z' &= Az + B \\ w' &= -z \end{align}\]

再从齐次坐标变回来，得到 \((-\frac{nx}{z}, -\frac{ny}{z}, -A-\frac{B}{z})\)。可以看到，x 和 y 都得到了和前面用相似三角形计算出来一样的结果，但是 z 的值出现了变化。但是没有关系，虽然 z 的值变了，但是它依然是保序的，只需要继续保证它在 \([-f, -n]\) 范围即可：

\[\begin{align} -n = -A-\frac{B}{-n} \\ -f = -A-\frac{B}{-f} \end{align}\]

求解可得 \(A=n+f, B=-nf\)，因此前面的矩阵就是：

\[ \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & -1 & 0 \end{pmatrix} \]

到这一步，就完成了四棱台到长方体的映射，接下来就是正交投影了，把长方体映射到 NDC 上，因此最终整体的投影矩阵就是把两个矩阵乘起来（正交投影矩阵左乘上面的矩阵），得到的结果如下：

\[ \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{-2}{f-n} & -\frac{f+n}{f-n} \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & -1 & 0 \end{pmatrix} = \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{n+f}{f-n} & \frac{-2nf}{f-n} \\ 0 & 0 & -1 & 0 \end{pmatrix} \]

这就是最终的透视投影的矩阵。需要注意的是，它假设了输入的坐标的 \(w=1\)，如果输入的齐次坐标的 \(w \ne 1\)，计算结果就会有问题。在 OpenGL 中，可以用 gluPerspective() 函数得到它：

和上面的结果看似不同，但只要设定 \(r=-l, t=-b, f=\frac{n}{t}, aspect=\frac{r}{t}\)，两个矩阵就是一样的。也就是说 gluPerspective 采用了透视投影的特殊情况：左右和上下对称。

其中 aspect 是长宽比（x 轴除以 y 轴）；\(f=cot(\frac{fovy}{2})\) 是这么推导的：y 方向上的视野角度上下对称，角度大小是 \(fovy\)，那么在水平线上方的角度就是 \(\frac{fovy}{2}\)，而这个角度在三角形中，它的对边是 \(t\)，邻边是 \(n\)，所以 \(tan(\frac{fovy}{2})=\frac{t}{n}\)，反过来就得到 \(f=\frac{n}{t}=cot(\frac{fovy}{2})\)。

更加通用的 OpenGL 函数是 glFrustum，它得到的矩阵和上面推导出来的矩阵是一样的，没考虑特殊情况。

mesa 中的实现：

// Source: https://github.com/Mesa3D/mesa/blob/957009978ef6d7121fc0d710d03bc20097d4d46b/src/mesa/math/m_matrix.c#L773-L797
void
_math_matrix_frustum( GLmatrix *mat,
              GLfloat left, GLfloat right,
              GLfloat bottom, GLfloat top,
              GLfloat nearval, GLfloat farval )
{
   GLfloat x, y, a, b, c, d;
   GLfloat m[16];

   x = (2.0F*nearval) / (right-left);
   y = (2.0F*nearval) / (top-bottom);
   a = (right+left) / (right-left);
   b = (top+bottom) / (top-bottom);
   c = -(farval+nearval) / ( farval-nearval);
   d = -(2.0F*farval*nearval) / (farval-nearval);  /* error? */

#define M(row,col)  m[col*4+row]
   M(0,0) = x;     M(0,1) = 0.0F;  M(0,2) = a;      M(0,3) = 0.0F;
   M(1,0) = 0.0F;  M(1,1) = y;     M(1,2) = b;      M(1,3) = 0.0F;
   M(2,0) = 0.0F;  M(2,1) = 0.0F;  M(2,2) = c;      M(2,3) = d;
   M(3,0) = 0.0F;  M(3,1) = 0.0F;  M(3,2) = -1.0F;  M(3,3) = 0.0F;
#undef M

   matrix_multf( mat, m, MAT_FLAG_PERSPECTIVE );
}

View 矩阵

OpenGL 中，经过 Model 和 View 矩阵映射后得到 Eye Coordinates，相机位于 (0, 0, 0)，且看向 -Z 轴的方向。计算相机 View 矩阵的 OpenGL 函数是 gluLookAt。

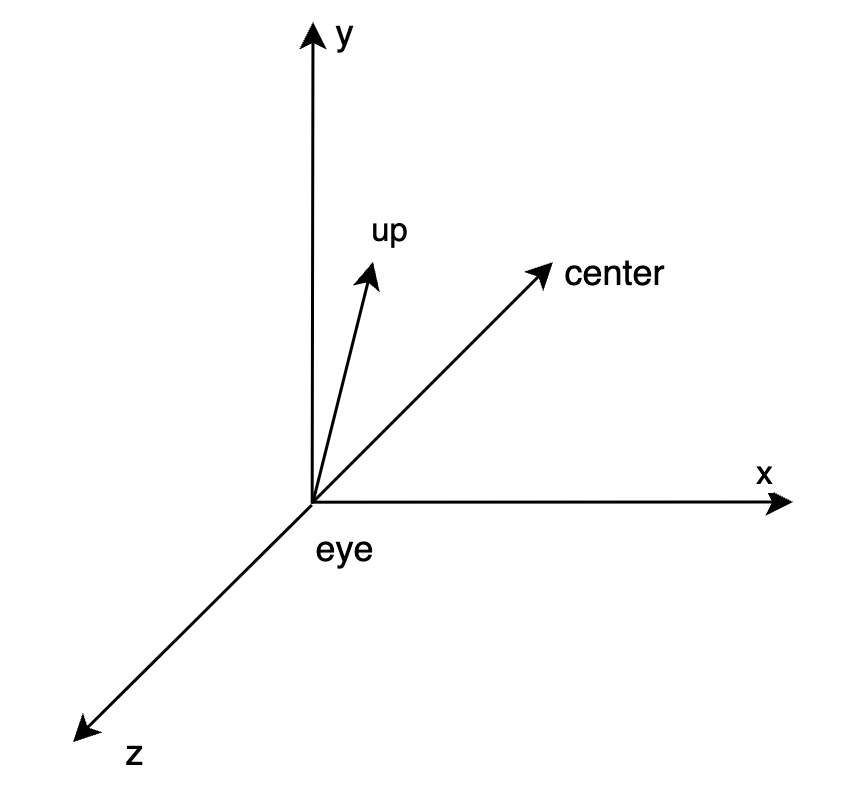
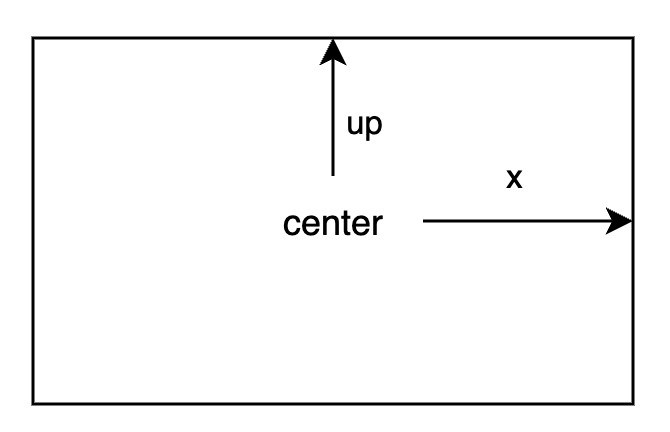
在映射之前，相机位于世界坐标的 (eyeX, eyeY, eyeZ)，视线看向 (centerX, centerY, centerZ) 点（视野正前方），以及视野里向上的方向在 3D 里的向量 (upX, upY, upZ)（视野的上方，y 轴）。

那么相机正对的向量 F=(centerX-eyeX, centerY-eyeY, centerZ-eyeZ)，这个方向在映射后的坐标系中就是 -Z 轴。令 UP=(upX, upY, upZ)，UP 最终在视野里看到的是沿 y 轴向上，但是映射以后可能会有 z 的分量，也就是 F 和 UP 不一定垂直，后面需要考虑这一点。

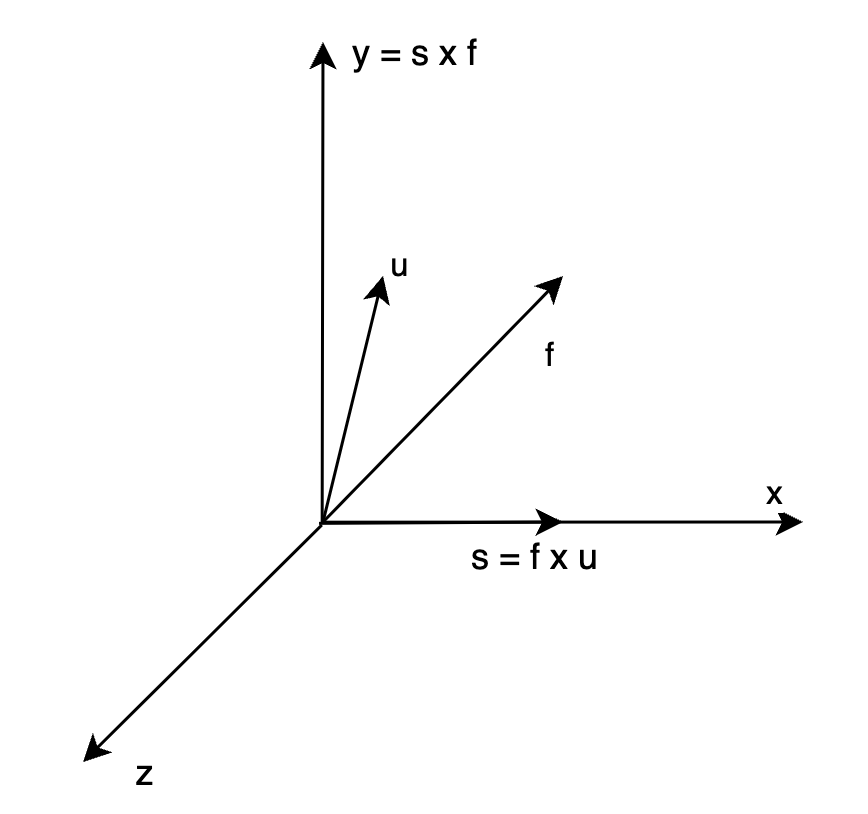
对 \(F\) 进行标准化，得到 \(f\)；对 UP 进行标准化，得到 \(u\)；由于 \(u\) 和 \(f\) 确定了 Y-Z 平面，所以求 X 方向的向量，直接计算叉积即可：\(s = f \times u\)，由于 \(f\) 指向 -Z，\(u\) 在 Y-Z 平面中 Y 为正的半平面，所以得到的 s 指向的是屏幕的右侧，不妨规定右侧是 X 正半轴（右手系）。此时再叉积，得到 Y 轴的方向：\(y = s \times f\)。

此时三个轴上的向量都有了：X 轴正方向是 s，Y 轴正方向是 y，Z 轴负方向是 f。由于叉积以前已经做了标准化，所以这三个向量都是单位向量。那么坐标系的变换矩阵应该实现下面的映射：

\(Ms = M(s_x, s_y, s_z)^T = (1, 0, 0)^T\)
\(My = M(y_x, y_y, y_z)^T = (0, 1, 0)^T\)
\(Mz = M(f_x, f_y, f_z)^T = (0, 0, -1)^T\)

于是：

\[ M=\begin{pmatrix} s_x & s_y & s_z \\ y_x & y_y & y_z \\ -f_x & -f_y & -f_z \\ \end{pmatrix} \]

这里依赖了三个向量 \(s\) \(y\) \(-f\) 都是单位向量，且互相正交的性质。

把齐次坐标的 w 维度加回来，就是：

\[ M=\begin{pmatrix} s_x & s_y & s_z & 0 \\ y_x & y_y & y_z & 0 \\ -f_x & -f_y & -f_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

以上矩阵解决了相机坐标系的问题，剩下就是把坐标 (eyeX, eyeY, eyeZ) 挪到 (0, 0, 0) 上：

\[ M=\begin{pmatrix} s_x & s_y & s_z & 0 \\ y_x & y_y & y_z & 0 \\ -f_x & -f_y & -f_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -\mathrm{eyeX} \\ 0 & 1 & 0 & -\mathrm{eyeY} \\ 0 & 0 & 1 & -\mathrm{eyeZ} \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

这样就得到了完整的 View 矩阵。

mesa 中的实现：

// Source: https://gitlab.freedesktop.org/mesa/mesa/-/blob/c6a80dc32ef17bc972d4137ce7444ebed4d28ebb/src/glu/sgi/libutil/project.c#L108
// Comments added
void gluLookAt(GLdouble eyex, GLdouble eyey, GLdouble eyez, GLdouble centerx,
    GLdouble centery, GLdouble centerz, GLdouble upx, GLdouble upy,
    GLdouble upz)
{
    float forward[3], side[3], up[3];
    GLfloat m[4][4];

    /* Compute f = center - eye */
    forward[0] = centerx - eyex;
    forward[1] = centery - eyey;
    forward[2] = centerz - eyez;

    up[0] = upx;
    up[1] = upy;
    up[2] = upz;

    normalize(forward);

    /* Side = forward x up */
    cross(forward, up, side);
    normalize(side);

    /* Recompute up as: up = side x forward */
    cross(side, forward, up);

    __gluMakeIdentityf(&m[0][0]);

    /* s_x s_y s_z */
    m[0][0] = side[0];
    m[1][0] = side[1];
    m[2][0] = side[2];

    /* y_x y_y y_z */
    m[0][1] = up[0];
    m[1][1] = up[1];
    m[2][1] = up[2];

    /* -f_x -f_y -f_z */
    m[0][2] = -forward[0];
    m[1][2] = -forward[1];
    m[2][2] = -forward[2];

    /* Update view matrix */
    glMultMatrixf(&m[0][0]);
    glTranslated(-eyex, -eyey, -eyez);
}

光线追踪

Whitted-style ray-tracing 是一种典型的光线追踪算法，它的实现思路是：

对于要绘制在屏幕上的点，计算它在 3 维空间中的对应的位置，与相机的原点构成一个射线
计算射线与场景中表面的第一个交点，根据表面的类型进行不同的处理：
1. 漫反射（Diffuse）：找到所有的光源，找出那些可以照亮交点的光源（光源到交点之间没有遮挡），计算出光源对这一点的贡献
2. 镜面反射（Specular）：计算出反射光，把反射光当成视线，继续递归
3. 镜面反射 + 折射（Refraction）：分别计算出反射光和折射光，分别递归然后按照 Fresnel 方程加权求和

可以看到，所有的光线在递归终止的时候，要么是在漫反射表面上，要么就是没有找到相交的表面。

辐射度量学

参考路径追踪（Path Tracing）与渲染方程 (Render Equation) 和 GAMES101 Lecture 15：

Radiant energy Q：光源向空间中辐射的能量，单位是 J
Radiant flux(power) \(\Phi\)：光源在单位时间内向空间中辐射的能量，单位是 W
Solid angle \(\omega\)：立体角，单位是 steradian/square radian 球面度，简写 sr；是在球面上一个小平面的面积除以半径的平方，即 \(\omega=A/r^2\)
Radiant intensity I：光源在单位立体角内的 Radiant flux，单位是 W/sr
Irradiance E：单位面积接受到的 Radiant flux，即 \(E=\Phi/A\)，单位是 \(W/m^2\)
Radiance L：单位面积下，接收到来自单位立体角的 Radiant flux，单位是 \(W/sr \cdot m^2\)

Rendering equation

参考 GAMES101 Lecture 15：

\[ L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{\Omega} L_i(p, \omega_i) f_r(p, \omega_i, \omega_o) (n \cdot \omega_i) \mathrm{d} \omega_i \]

含义：从平面上的 \(p\) 点出发，向 \(\omega_r\) 发射的 Radiance 包括两部分：

\(L_e(p, \omega_o)\)：这个点本身发的光，例如光源
\(\int_{\Omega} L_i(p, \omega_i) f_r(p, \omega_i, \omega_o) (n \cdot \omega_i) \mathrm{d} \omega_i\)：考虑半球面上的任意一个入射方向 \(\omega_i\)，这个方向上入射到 \(p\) 点的 Radiance 是 \(L_i(p, \omega_i)\)，其中有一定比例会反射到 \(\omega_o\) 方向上，这个比例就是 BRDF \(f_r(p, \omega_i, \omega_o)\)，最后由于入射方向和平面的法方向有一个夹角 \(\theta\)，根据 Lambert's Cosine Law，需要乘上 \(\cos \theta = n \cdot \omega_i\) 项。

Bidirectional reflectance distribution function

BRDF（Bidirectional reflectance distribution function）指的是在一个表面上，特定角度（\(\omega_i\)）的入射光有多大比例会被反射到特定角度（\(\omega_o\)）的出射光。

常见的 BRDF 有：

Lambertian：一般用于漫反射表面，光均匀反射到各个角度，因此和出射角度无关：\(f=c/\pi\)，其中 \(c\) 是表面的颜色，除以 \(\pi\) 是为了满足能量守恒，计算过程见 Deriving Lambertian BRDF from first principles
Phong 和 Blinn-Phong：用于 OpenGL Fixed-function pipeline
Cook-Torrance：\(f=k_d\frac{c}{\pi} + k_s\frac{DFG}{4(n \cdot \omega_i)(n \cdot \omega_o)}\)，前面的 \(k_d\frac{c}{\pi}\) 和 Lambertian 一样，后面的 \(DFG\) 表示三个函数的乘积，分别是 Normal Distribution Function，Fresnel Function 和 Geometric Attenuation Function，详见 Physically-Based Rendering Cook-Torrance Reflectance Model 和 LearnOpenGL CN - Theory

图形 API 对比

下面给出不同图形 API 或者库在约定上的不同：

	OpenGL	Direct3D	Metal	Vulkan
NDC 采用	左手系	左手系	左手系	右手系
NDC 中 z 的范围	[-1, 1]	[0, 1]	[0, 1]	[0, 1]
NDC (-1, -1) 在	左下角	左下角	左下角	左上角
Framebuffer (0,0) 在	左下角	左上角	左上角	左上角

参考：

另外还推荐阅读：

What are the coordinates?

抗锯齿/超分辨率/帧生成

SSAA(Super Sampling Anti Aliasing)/FSAA(Full Scene Anti Aliasing): 按更高的分辨率渲染，再降采样到屏幕分辨率，计算量很大。
MSAA(Multi Sampling Anti Aliasing)：按更高的分辨率来进行覆盖测试和深度测试，即一个像素有多个采样点，每个采样点都要找到覆盖了这个点的三角形，但每个三角形只进行一次着色（SSAA 是每个采样点进行一次着色），着色结果会复制到这个三角形覆盖的所有采样点上。如果有多个三角形覆盖了不同的采样点，最后相当于是按照覆盖的采样点个数加权平均。最坏情况下，每个采样点都属于不同的三角形，这时候性能会退化为 SSAA，但大多数情况，一个像素的多个采样点属于同一个三角形，这时候性能就很好。
NVIDIA DLSS(Deep Learning Super Sampling) 1.0：按更低的分辨率渲染，用 AI 进行超分辨率，再降采样到屏幕分辨率上，例如 1920x1080 渲染，AI 超分辨率到 15360x8640，再降采样到 3840x2160。每个游戏需要专门训练模型，经过 AI 超分辨率，一个像素变成 64 个像素。
NVIDIA DLSS(Deep Learning Super Sampling) 2.0：和 DLSS 1.0 不同，DLSS 2.0 是一种 TAAU（Temporal Anti Aliasing Upscaling）算法，Temporal 意思是利用了多帧的信息，去预测高分辨率的输出。DLSS 2.0 支持不同的超分辨率档位：Quality 就是按照长宽各是原来 66.7% 的分辨率去渲染，Balanced 是 58.0%，Performance 是 50.0%。用低分辨率渲染以后，再用通用的 AI 超分辨率网络，不再需要给每个游戏训练单独的网络。
NVIDIA DLSS(Deep Learning Super Sampling) 3.0：引入了帧生成技术，每渲染一张图，就生成出新的一张图，即有一半的图像是生成出来的。
NIS(NVIDIA Image Scaling)：开源的图形缩放和锐化算法，非 AI，无时序信息。用低分辨率渲染，再用 NIS 进行放大，即实现了超分辨率。
AMD FSR(FidelityFX Super Resolution) 1：和 NIS 类似，开源的图形缩放和锐化算法，非 AI，无时序信息。前身是 Fidelity Contrast Adaptive Sharping（CAS）锐化技术。
AMD FSR(FidelityFX Super Resolution) 2：开源的图形缩放和锐化算法，非 AI，引入了时序信息。
AMD FSR(FidelityFX Super Resolution) 3：开源的图形缩放和锐化算法，非 AI，引入了时序信息和帧生成。
AFMF(AMD Fluid Motion Frames)：在 AMD 驱动上实现的帧生成，软件无感知。
Intel XeSS(Xe Super Sampling)：开源，类 DLSS，用 AI 进行超分辨率。

参考：

计算机图形学

齐次坐标

坐标变换

Normalized Device Coordinates

正交投影

透视投影

View 矩阵

光线追踪

辐射度量学

Rendering equation

Bidirectional reflectance distribution function

图形 API 对比

抗锯齿/超分辨率/帧生成

评论