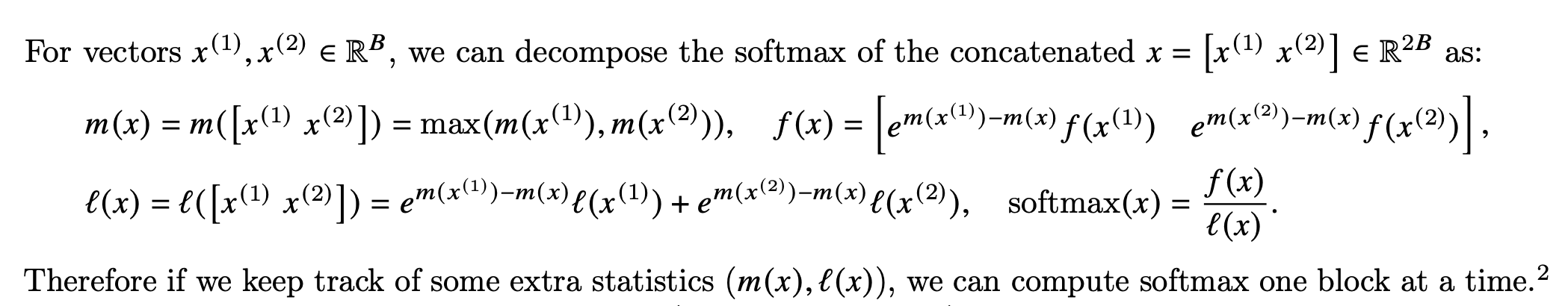跳转至

Transformer

下面只考虑 Decoder-only 的 Transformer。

计算过程

输入 \(n\) 个 Token，通过 Text 和 Position Embedding 后，得到一个尺寸为 \((n, d_{model})\) 的矩阵，其中 \(d_{model}\) 为 Embedding 向量的长度。

接着，经过 \(n_{layer}\) 个层，每层中要进行如下的计算：

  1. 从上一层的输出 \((n, d_{model})\)，每个 head 上乘以三个 \((d_{model}, d_{head})\) 的矩阵，得到 Q，K 和 V，尺寸为 \((n, d_{head})\)
  2. 按照 attention 激活公式，得到 Z，尺寸为 \((n, d_{head})\)
  3. 把所有 head 的 Z 矩阵拼起来，保证 \(d_{model} = n_{head} * d_{head}\)，那么所有的 Z 拼起来以后得到的矩阵的尺寸为 \((n, d_{head})\)
  4. 乘以一个尺寸为 \((d_{model}, d_{model})\) 的 Projection 矩阵，得到新矩阵 \((n, d_{model})\)
  5. 经过一个 MLP，MLP 第一层是 \((d_{model}, 4*d_{model})\)，第二层是 \((4*d_{model}, d_{model})\)
  6. MLP 输出的矩阵尺寸为 \((n, d_{model})\)

KV cache

在推理的时候，是在已有的 context 的基础上，生成一个新 token，再把 token 加到 context，继续生成下一个 token。计算的时候，由于 Attention 会带 Mask，旧 token 不会依赖新 token，因此旧 token 的部分不会变，可以只考虑新引入的 token 带来的变化。

那么，计算新的 token 的 Q K V 以后，在进行 Attention 计算的时候，会发现先前的 token 的 K 和 V 部分不变，先前 token 的 Q 不影响当前 token 的结果。因此可以把之前 token 的 K 和 V 保存下来，不用重新计算，这就是 KV cache。

参数量和浮点计算量

考虑每层的参数量和浮点计算量：

  1. 计算 Q，K 和 V：参数是三个 \((d_{model}, d_{model})\) 的矩阵，计算量是 \(2 * 3 * n * d_{model}^2\)
  2. 乘以 Projection 矩阵：参数是 \((d_{model}, d_{model})\) 的矩阵，计算量是 \(2 * n * d_{model}^2\)
  3. 乘以 MLP 第一层：参数是 \((d_{model}, 4*d_{model})\) 的矩阵，计算量是 \(2 * 4 * n * d_{model}^2\)
  4. 乘以 MLP 第二层：参数是 \((4*d_{model}, d_{model})\) 的矩阵，计算量是 \(2 * 4 * n * d_{model}^2\)

其余部分的参数量和计算量可以忽略不计。

因此总参数量（不考虑 Embedding）为：

\[ 12n_{layer}d_{model}^2 \]

每个 Token 的浮点计算量为：

\[ 24n_{layer}d_{model}^2 \mathrm{FLOP} \]

Llama 2 7B

以 Llama 2 7B 为例，下面分析 Transformer 推理的计算过程，它的参数如下：

  • hidden size: 4096
  • intermediate size（MLP 的中间层的维度）: 11008
  • hidden layers: 32
  • attention heads: 32
  • key value heads: 32
  • head dim: 4096 / 32 = 128
  • vocab size: 32000

参考 HuggingFace 源码。

Llama2 的主要计算过程是 32 层 LlamaDecoderLayer，每个 LlamaDecoderLayer 包括：

  1. hidden_states = self.input_layernorm(hidden_states): 见 LlamaRMSNorm
  2. hidden_states, self_attn_weights, present_key_value = self.self_attn()：见 LlamaAttention
  3. hidden_states = residual + hidden_states: aten::add([1, 1, 4096], [1, 1, 4096]) = [1, 1, 4096]
  4. hidden_states = self.post_attention_layernorm(hidden_states): 见 LlamaRMSNorm
  5. hidden_states = self.mlp(hidden_states)：见 LlamaMLP
  6. hidden_states = residual + hidden_states: aten::add([1, 1, 4096], [1, 1, 4096]) = [1, 1, 4096]

hidden_states 的规模是 [1, 1, 4096]。

LlamaRMSNorm 包括：

  1. hidden_states = hidden_states.to(torch.float32): aten::to([1, 1, 4096]) = [1, 1, 4096]
  2. v1 = hidden_states.pow(2): aten::pow([1, 1, 4096]) = [1, 1, 4096]
  3. variance = v2.mean(-1, keepdim=True): aten::mean([1, 1, 4096]) = [1, 1, 1]
  4. v3 = variance + self.variance_epsilon: aten::add([1, 1, 1]) = [1, 1, 1], 1 FLOP
  5. v4 = torch.rsqrt(v3): aten::rsqrt([1, 1, 1]) = [1, 1, 1]
  6. hidden_states = hidden_states * v4: aten::mul([1, 1, 4096], [1, 1, 1]) = [1, 1, 4096], 4096 FLOP
  7. v5 = hidden_states.to(input_dtype): aten::to([1, 1, 4096]) = [1, 1, 4096]
  8. return self.weight * v5: aten::mul([4096], [1, 1, 4096]), 4096 FLOP

LlamaAttention 包括：

  1. query_states = self.q_proj(hidden_states): aten::linear([1, 1, 4096], [4096, 4096]) = [1, 1, 4096], 33554432 FLOP
  2. key_states = self.k_proj(hidden_states): aten::linear([1, 1, 4096], [4096, 4096]) = [1, 1, 4096], 33554432 FLOP
  3. value_states = self.v_proj(hidden_states): aten::linear([1, 1, 4096], [4096, 4096]) = [1, 1, 4096], 33554432 FLOP
  4. v1 = query_states.view(bsz, q_len, self.num_heads, self.head_dim): aten::view([1, 1, 4096]) = [1, 1, 32, 128]
  5. query_states = v1.transpose(1, 2): aten::transpose([1, 1, 32, 128]) = [1, 32, 1, 128]
  6. v2 = key_states.view(bsz, q_len, self.num_key_value_heads, self.head_dim): aten::view([1, 1, 4096]) = [1, 1, 32, 128]
  7. key_states = v2.transpose(1, 2): aten::transpose([1, 1, 32, 128]) = [1, 32, 1, 128]
  8. v3 = value_states = value_states.view(bsz, q_len, self.num_key_value_heads, self.head_dim): aten::view([1, 1, 4096]) = [1, 1, 32, 128]
  9. value_states = v3.transpose(1, 2): aten::transpose([1, 1, 32, 128]) = [1, 32, 1, 128]
  10. cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len): 见 LlamaRotaryEmebdding
  11. query_states, key_states = apply_rotary_pos_emb(query_states, key_states, cos, sin, position_ids): 见 apply_rotary_pos_emb
  12. key_states = torch.cat([past_key_value[0], key_states], dim=2): aten::cat([1, 32, C-1, 128], [1, 32, 1, 128]) = [1, 32, C, 128]
  13. value_states = torch.cat([past_key_value[1], value_states], dim=2): aten::cat([1, 32, C-1, 128], [1, 32, 1, 128]) = [1, 32, C, 128]
  14. v4 = key_states.transpose(2, 3): aten::transpose([1, 32, C, 128]) = [1, 32, 128, C]
  15. v5 = torch.matmul(query_states, v4): aten::matmul([1, 32, 1, 128], [1, 32, 128, C]) = [1, 32, 1, C], 8192*C FLOP
  16. attn_weights = v1 / math.sqrt(self.head_dim): aten::div([1, 32, 1, C]) = [1, 32, 1, C]
  17. attn_weights = attn_weights + attention_mask: aten::add([1, 32, 1, C], [1, 1, 1, C]) = [1, 32, 1, C], 32*C FLOP
  18. v6 = nn.functional.softmax(attn_weights, dim=-1, dtype=torch.float32).to(query_states.dtype): aten::softmax([1, 32, 1, C]) = [1, 32, 1, C]
  19. attn_weights = v6.to(query_states.dtype): aten::to([1, 32, 1, C]) = [1, 32, 1, C]
  20. attn_output = torch.matmul(attn_weights, value_states): aten::matmul([1, 32, 1, C], [1, 32, C, 128]) = [1, 32, 1, 128]: 8192*C FLOP
  21. attn_output = attn_output.transpose(1, 2).contiguous(): aten::transpose([1, 32, 1, 128]) = [1, 1, 32, 128]
  22. attn_output = attn_output.reshape(bsz, q_len, self.hidden_size): aten::reshape([1, 1, 32, 128]) = [1, 1, 4096]
  23. attn_output = self.o_proj(attn_output): aten::linear([1, 1, 4096], [4096, 4096]) = [1, 1, 4096], 33554432 FLOP

LlamaRotaryEmbedding 包括：

  1. self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),: aten::slice([1, 1, 4096, 128])
  2. self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype),: aten::slice([1, 1, 4096, 128])

apply_rotary_pos_emb 包括：

  1. v1 = cos.squeeze(1): aten::squeeze([1, 1, 10, 128])
  2. cos = v1.squeeze(0): aten::squeeze([1, 10, 128])
  3. v2 = cos.squeeze(1): aten::squeeze([1, 1, 10, 128])
  4. sin = v2.squeeze(0): aten::squeeze([1, 10, 128])
  5. v3 = cos[position_ids]: aten::index([10, 128])
  6. cos = v3.unsqueeze(1): aten::unsqueeze([1, 1, 128]) = [1, 1, 1, 128]
  7. v4 = sin[position_ids]: aten::index([10, 128])
  8. sin = v4.unsqueeze(1): aten::unsqueeze([1, 1, 128]) = [1, 1, 1, 128]
  9. v5 = q * cos: aten::mul([1, 32, 1, 128], [1, 1, 1, 128]) = [1, 32, 1, 128], 4096 FLOP
  10. v6 = rotate_half(q): 见 rotate_half
  11. v7 = v6 * sin: aten::mul([1, 32, 1, 128], [1, 1, 1, 128]) = [1, 32, 1, 128], 4096 FLOP
  12. q_embed = v5 + v7: aten::add([1, 32, 1, 128], [1, 32, 1, 128]) = [1, 32, 1, 128], 4096 FLOP
  13. v8 = k * cos: aten::mul([1, 32, 1, 128], [1, 1, 1, 128]) = [1, 32, 1, 128], 4096 FLOP
  14. v9 = rotate_half(k): 见 rotate_half
  15. v10 = v9 * sin: aten::mul([1, 32, 1, 128], [1, 1, 1, 128]) = [1, 32, 1, 128], 4096 FLOP
  16. k_embed = v8 + v10: aten::add([1, 32, 1, 128], [1, 32, 1, 128]) = [1, 32, 1, 128], 4096 FLOP

rotate_half 包括：

  1. x1 = x[..., : x.shape[-1] // 2]: aten::slice([1, 3, 1, 128])
  2. x2 = x[..., x.shape[-1] // 2 :]: aten::slice([1, 3, 1, 128])
  3. v1 = -x2: aten::neg([1, 3, 1, 64])
  4. return torch.cat((v1, x1), dim=-1): aten::cat([1, 3, 1, 64], [1, 3, 1, 64]) = [1, 3, 1, 128]

LlamaMLP 包括：

  1. v1 = self.gate_proj(x): aten::linear([1, 1, 4096], [11008, 4096]) = [1, 1, 11008], 90177536 FLOP
  2. v2 = self.act_fn(v1): aten::silu([1, 1, 11008]) = [1, 1, 11008]
  3. v3 = self.up_proj(x): aten::linear([1, 1, 4096], [11008, 4096]) = [1, 1, 11008], 90177536 FLOP
  4. v4 = v2 * v3: aten::mul([1, 1, 11008], [1, 1, 11008]) = [1, 1, 11008], 11008 FLOP
  5. v5 = self.down_proj(v4): aten::linear([1, 1, 11008], [4096, 11008]) = [1, 1, 4096], 90177536 FLOP

最后一个 LlamaDecoderLayer 的输出会经过 lm_head 得到 logits：

  1. logits = self.lm_head(hidden_states): aten::linear([1, 1, 4096], [32000, 4096]) = [1, 1, 32000], 262144000 FLOP

所有 aten 算子：

  • aten::add
  • aten::cat
  • aten::div
  • aten::index
  • aten::linear
  • aten::matmul
  • aten::mean
  • aten::mul
  • aten::neg
  • aten::pow
  • aten::reshape
  • aten::rsqrt
  • aten::sequeeze
  • aten::silu
  • aten::slice
  • aten::softmax
  • aten::to
  • aten::transpose
  • aten::unsqueeze
  • aten::view

FlashAttention

论文：FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

代码：Dao-AILab/flash-attention

推荐阅读：FlashAttention 核心逻辑以及 V1 V2 差异总结

主要针对 Transformer 训练中的 Attention 计算进行优化。Attention 计算的是：

\(S = QK^T, P = \mathrm{softmax}(S), O = PV\)

其中 Q、K 和 V 矩阵规模都是 \(N*d\)，S 和 P 矩阵规模是 \(N*N\)，O 矩阵规模是 \(N*d\)，N 是序列长度，d 是 head dimension。实际上 \(S\) 矩阵还会除以一个系数，但是这个优化起来比较简单，就忽略了。朴素算法就是这三个步骤分别算，但是就比较慢。核心问题是 softmax 操作。softmax 的定义是：

\(\mathrm{softmax}(x) = \frac{e^{x_i}}{\Sigma_j e^{x_j}}\)

分子是对应项的 exp，分母是所有项的 exp 之和。所以 softmax 的按定义算的方法就是：所有元素求 exp，然后求 exp 的和，再集体做除法。

但是这么算会有一个问题：元素的 exp 可能会很大，导致精度比较差。因此实际计算的时候，会先计算出元素的最大值 \(x_m\)，然后分子分母同时除以最大值的 exp：

\(\mathrm{softmax}(x) = \frac{e^{x_i-x_m}}{\Sigma_j e^{x_j-x_m}}\)

这样计算的精度会比较好，因为 exp 的值都在 0 和 1 之间。这也意味着 softmax 的计算需要先求 max，然后每个元素减去 max 后，求 exp，再求元素的 exp 之和，最后每个元素再除以 exp 之和。准确地说，因为这里的输入是矩阵，所以是对矩阵的每一行分别算 softmax。

但是这样的求法意味着需要先把完整的 softmax 输入求出来，使得 tiling 变得困难。为了 tiling，FlashAttention 采用了一种分块的 softmax 计算方法：首先对每一块分别做 softmax，但是按照定义，max 和 sum 都应该是完整向量的 max 和 sum，而如果分块去计算 softmax，此时的 max 和 sum 是块内的，因此需要进行后处理，把分块的 softmax 纠正成正确的 softmax：

假如有两个块分别做了 softmax，结果是两个向量 \(x_1\) 和 \(x_2\)，计算时的 max 记为 \(m_1\) 和 \(m_2\)，分子记为 \(f(x_1)\) 和 \(f(x_2)\)，分母记为 \(l(x_1)\) 和 \(l(x_2)\)。那么合并后的向量的 max 就是 \(m=\max(m_1, m_2)\)，接下来计算出完整的 softmax：分子来自于两个向量，但是需要把 \(m_1\) \(m_2\) 和 \(m\) 的差异补上，那就是 \(e^{m_1-m}f(x_1)\) 和 \(e^{m_2-m}f(x_2)\) 两部分拼接起来；分母则是两个向量的部分，把 max 差异纠正后再求和：\(e^{m_1-m}l(x_1)+e^{m_2-m}l(x_2)\)。论文中是这么表示的：

分块 softmax（来源：FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness）

因此计算 softmax 的时候可以先分块进行，最后再把结果纠正过来。能分块了以后，就可以做 kernel fusion，和矩阵乘法、Masking、Dropout 合并起来，让中间结果在 GPU 内部完成，而不是先写到显存里再读回来。

论文的 Algorithm 1 和 2 给出了融合后的 Kernel 的伪代码。思路是：

  1. 对 Q、K 和 V 分块
  2. 对于每个块，计算当前块的 \(QK^T\) 结果，然后计算 rowmax（每行计算出一个最大值），每个元素减去 rowmax 再 exp，得到 softmax 函数的分子；再求和，得到 softmax 函数的分母
  3. 把刚算出来的 softmax 结果和之前计算的 softmax 结果合并，得到一组新的 softmax 系数
  4. 更新当前的输出矩阵：把旧的分母乘回来，就得到旧的分子，把旧的分子乘上 exp 系数，再加上新的分子，结果再除以新的分子；这一步和迭代更新平均值很像：旧的平均值乘以旧的元素个数，加上新的元素再除以新的元素个数

然后在中间穿插 dropout 和 masking 等细节，就得到了最终的实现。对这个过程讲的比较清楚的是下面这个图：

Flash Attention（来源：FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning）

右下角 Rescaling to correct denominator 就是上面说的，把旧的分母乘回来，再计算出新的值。标量乘矩阵在上面的式子里表示成了对角矩阵和矩阵的乘法。

不过，这份伪代码距离实际的 CUDA 实现，还有很多细节上的优化。此外，论文还对梯度反向传播进行了优化，毕竟是服务于训练：思路是，前向计算的时候，因为 kernel fusion 的原因，跳过了中间结果的运算，所以反向传播的时候，就重新计算一下 attention，再求梯度。

FlashAttention 2

论文：FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning

代码：Dao-AILab/flash-attention

FlashAttention 2 相比 FlashAttention 的主要区别是并行的方式。第一个版本是在 batch 和 head 维度上进行并行，也就是说，每个 CUDA thread block 对应一个 batch size 和一个 attention head，一共有 batch size 乘以 head 个数那么多个 thread block。

而第二个版本在 sequence length 维度上也引入了并行，使得 GPU 的利用率可以继续提升。此外，在计算局部 softmax 的时候，也做了修改：不着急计算局部的 softmax，而是分别维护分子和分母，到算完了以后，再算分子除以坟墓。

FlashDecoding

博客：Flash-Decoding for long-context inference

Flash Decoding 是针对长上下文场景下的推理：KV cache 的读取变成了一个瓶颈。所以 Flash-Decoding 的思路就是，并行读取 KV-cache，并且在 sequence length 维度上并行 attention 计算。当然了，并行了以后，就要拆成多块分别求 softmax，也需要 Flash Attention 的合并方法来保证最终 softmax 结果的正确性。

FlashDecoding++

论文：FLASHDECODING++: FASTER LARGE LANGUAGE MODEL INFERENCE ON GPUS

这篇论文也是针对 transformer 推理的优化，主要的优化点：

  1. Flash Attention 论文解决了 softmax 的分块计算问题，但是每次需要计算一个 max；FlashDecoding++ 选择根据数据的分布去估计一个 max，之后再纠正，可以减少一些同步
  2. 针对 batch 维度小的矩阵乘法进行优化

参考文献

评论